Inferential Stats. Chapter-3)

What is Correlation?

Correlation in statistics is a way to measure the relation between two variables in terms of numbers. e.g. Degree of atmospheric pressure is negatively correlated to current height spot.

Correlation can be positive, negative or zero between two variables and correlation should be between -1 and 1. As we can say that correlation is a metric that describes the strength of the relation, if the value gets closer to 1; that means the strong positive relation and if the value gets closer to -1; that means the strong negative relation. Before we can make correlational assumptions we first need to explore most common technique developed by Karl Pearson. Below we will explore how to calculate correlation coefficient and conditions to provide while using.

Pearson's Correlation Coefficient

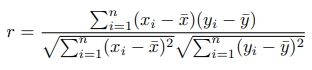
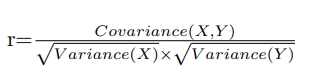
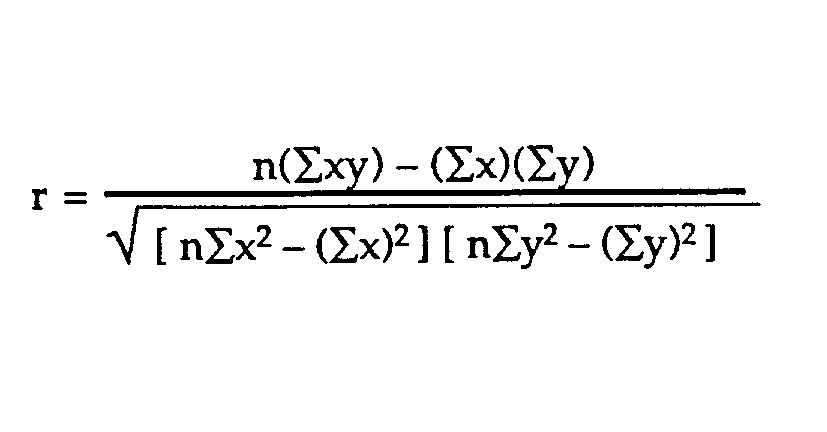
All three formulas mean the Pearson's Correlation Coefficient(r).

r= Correlation Coefficient
n= Number of total observations
x= Value on the x-axis
y= Value on the y-axis

x̄= Sample mean of x for given n value
ȳ= Sample mean of y for given n value

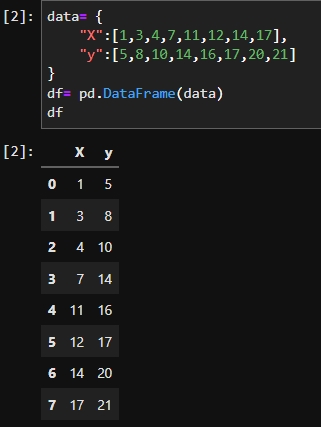
For a given dataset(or sample) we can use the formula to calculate the Pearson's Coefficient and we can see the relationship between two variables.Let's explore below dataset that includes the variables as x and y.

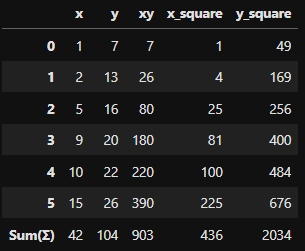
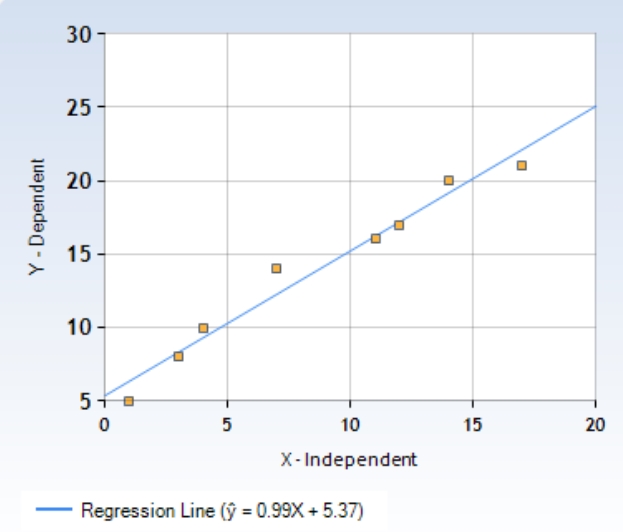
With applying above dataset to formulas we find the Pearson's Correlation Coefficient(r) as;

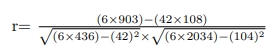
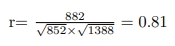
When and how to use Correlation Coefficient?

First thing to know is correlation coefficient can be used as en estimate of relation between variables. With saying that, more data you have more accurate relations you can find. e.g. The same r=-0.74 point should be more powerful with 10.000 samples than 10 samples. The trick here is the lower p-value. The lower p-value in the dataset helps to make relatively more accurate estimations about relations.
Correlation is calculated between two variables.
Don't use Pearson's Correlation if there's a non-linear relationship.
Pearson's Correlation is only sensitive to non-outlier normally distributed data.

What is Regression?

Regression Analysis is basically using independent variables(X,X1,X2..) to explain the changes in the dependent variable(Y). Regression Analysis can be named as the Foundation of Machine Learning Techniques because we can make predictions of the target variable(Y) for the given data points(X,X1,X2..) using Regression.

Simplest form of Regression is the Linear Regression. As it can be understood from the name, it is actually fitting a "line" to the 2 dimensions(x,y) Cartesian coordinate system. The technique is called Least Squares Residual.

Here is a sample data with the mean y value is 13.875

Since the definition of Linear Regression is basically explaining the variance with independent variables, firstly let's explore the variance around mean.

The line seen in the plot is the mean y value(13.875), and we are seeing the variance around the mean. If any line that fits data with smaller errors, that will be the "best fit" for our problem.
For Linear Regression problem; as we are going to fit a line, there is a line formula that "everybody" knows: y=aX+b
There is a derivative calculation for the best fit line, but computers are here for that. The things we should learn is what is the slope and the coefficient in the linear regression formula.
a is the slope of the line. b is the coefficient(the point where the line intersects the y-axis)

As seen on the plot, after the least squares calculation this line is the best fit for the dataset. The formula of the line is 0.98586X+5.37194
From this link you can make a Linear Regression model with your own dataset and try it for yourself.

Correlation and Regression

What is Correlation?

Pearson's Correlation Coefficient

When and how to use Correlation Coefficient?

What is Regression?